Démos sur le calcul flottant
Sources
- Les modes d’arrondi : code C++
- Les autres démos : notebook Jupyter ou code Python
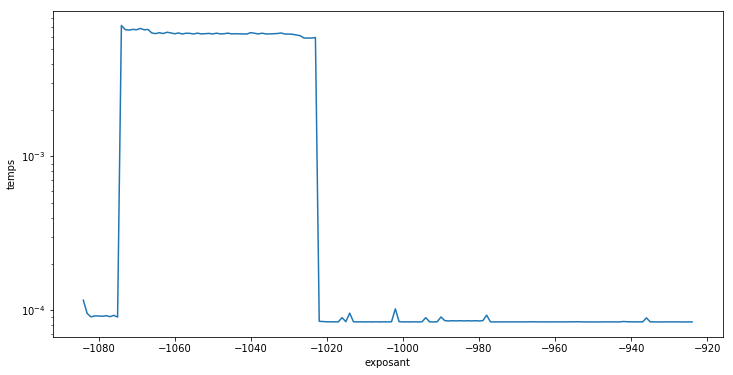
Performances des nombres sous-normaux
Pour tester la représentation en base 2 : https://www.h-schmidt.net/FloatConverter/IEEE754.html
import numpy as np
import time
import math
import matplotlib.pyplot as plt
%matplotlib inline
# Python utilise des nombres flottants à double précision (64 bits) :
# - signe sur 1 bit
# - mantisse de 53 bits (52 stockés)
# - exposant sur 11 bits (de -1024 à +1023)
e_max = -(1024-100)
e_min = -(1024+60) # Pour légèrement dépasser la capacité des nombres sous-normaux
N = 100000
duration = np.empty(e_max - e_min + 1)
for e in range(e_min, e_max+1):
values = (2**e) * np.ones(N)
tic = time.process_time()
r = values.sum()
duration[e - e_min] = time.process_time() - tic;
plt.figure(figsize=(12, 6))
plt.semilogy(range(e_min, e_max+1), duration)
plt.xlabel('exposant')
plt.ylabel('temps');
Approximation des réels
a = 10000.0
b = 9999.5
c = 0.1
print("{:.20f}".format(c))
0.10000000000000000555
a1 = a + c
print("{:.20f}".format(a1))
10000.10000000000036379788
print("{:.20f}".format(a1 - b))
0.60000000000036379788
print("{:.20f}".format(0.6))
0.59999999999999997780
Les modes d’arrondi
Le code en C++ :
#include <iostream>
#include <iomanip>
#include <cfenv>
int main()
{
double x = 1;
std::cout << std::setprecision(50);
std::fesetround(FE_TONEAREST); // Par défaut
std::cout << "Au plus proche: 1/10 = " << x/10 << std::endl;
std::cout << "Au plus proche: -1/10 = " << -x/10 << std::endl;
std::cout << std::endl;
std::fesetround(FE_DOWNWARD);
std::cout << "Vers -oo: 1/10 = " << x/10 << std::endl;
std::cout << "Vers -oo: -1/10 = " << -x/10 << std::endl;
std::cout << std::endl;
std::fesetround(FE_UPWARD);
std::cout << "Vers +oo: 1/10 = " << x/10 << std::endl;
std::cout << "Vers +oo: -1/10 = " << -x/10 << std::endl;
std::cout << std::endl;
std::fesetround(FE_TOWARDZERO);
std::cout << "Vers 0: 1/10 = " << x/10 << std::endl;
std::cout << "Vers 0: -1/10 = " << -x/10 << std::endl;
std::cout << std::endl;
return 0;
}
Le résultat :
Au plus proche: 1/10 = 0.1000000000000000055511151231257827021181583404541
Au plus proche: -1/10 = -0.1000000000000000055511151231257827021181583404541
Vers -oo: 1/10 = 0.099999999999999991673327315311325946822762489318847
Vers -oo: -1/10 = -0.10000000000000000555111512312578270211815834045411
Vers +oo: 1/10 = 0.10000000000000000555111512312578270211815834045411
Vers +oo: -1/10 = -0.099999999999999991673327315311325946822762489318847
Vers 0: 1/10 = 0.099999999999999991673327315311325946822762489318847
Vers 0: -1/10 = -0.099999999999999991673327315311325946822762489318847
Unit in the Last Place
def ulp(v):
print("{}\t{}".format(v, v - np.nextafter(v, v-1)))
ulp(1000)
ulp(100)
ulp(10)
ulp(1)
ulp(0.1)
ulp(0.01)
ulp(0)
1000 1.1368683772161603e-13
100 1.4210854715202004e-14
10 1.7763568394002505e-15
1 1.1102230246251565e-16
0.1 1.3877787807814457e-17
0.01 1.734723475976807e-18
0 5e-324
(1000 + 1.5e-12) - 1000
1.4779288903810084e-12
(1000 + 1e-14) - 1000
0.0
(1 + 1e-16) - 1
0.0
(1 + 2e-16) - 1
2.220446049250313e-16
(1 + 3e-16) - 1
2.220446049250313e-16
(1 + 4e-16) - 1
4.440892098500626e-16
Non associativité des opérations
0.1 + (0.2 - 0.3)
2.7755575615628914e-17
(0.1 + 0.2) - 0.3
5.551115123125783e-17
1 + 1e-17 - 1
0.0
1 - 1 + 1e-17
1e-17
Annulation catastrophique
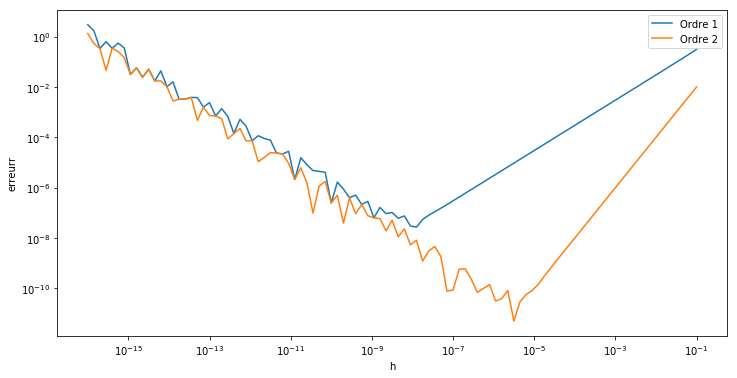
Différences finies
def f(x):
return x**3
def df(x):
return 3 * x**2
def deriv_fd1(f, x, h):
return (f(x+h) - f(x)) / h
def deriv_fd2(f, x, h):
return (f(x+h) - f(x-h)) / (2*h)
x = 1
h = np.logspace(-16, -1, 101)
err1 = abs(deriv_fd1(f, x, h) - df(x))
err2 = abs(deriv_fd2(f, x, h) - df(x))
plt.figure(figsize=(12, 6))
plt.loglog(h, err1)
plt.loglog(h, err2)
plt.legend(['Ordre 1', 'Ordre 2'])
plt.xlabel('h')
plt.ylabel('erreurr');
f(x)
1
f(x + 1e-9) # (1 + 1e-9)^3 = 1 + 3e-9 + 3e-18 + 1e-27
1.0000000030000002
f(x + 1e-9) - f(x - 1e-9) # = 6e-9 + 2e-27
6.000000163375319e-09
f(x + 1e-9) - f(x - 1e-9) - 6e-9 # = 2e-27
1.6337531864689604e-16
(f(x + 1e-9) - f(x - 1e-9)) / 2e-9 # = 3 + 1e-18
3.0000000816876593
Calcul des racines d’un polynôme du second degré
a = 1.
b = 1e4
c = 1.
# Calcul des racines
delta = b*b - 4*a*c
x = (-b - math.sqrt(delta)) / (2*a)
y = (-b + math.sqrt(delta)) / (2*a)
print("x = {}".format(x))
print("y = {}".format(y))
x = -9999.999899999999
y = -0.00010000000111176632
# Vérification
print("ax² + bx + c = {}".format(a*x*x + b*x + c))
print("ay² + by + c = {}".format(a*y*y + b*y + c))
ax² + bx + c = 0.0
ay² + by + c = -1.1176630732023796e-09
b*b
100000000.0
a*c
1.0
math.sqrt(b*b - 4*a*c)
9999.999799999998
$y=(-b+\sqrt{\delta})/(2*a)$ est mal calculé (soustraction de $2$ grands nombres proches, mais $x$ est bien calculé.
On sait que $x \times y = c / a$, d’où :
y = c / (x*a)
print("y = {}".format(y))
y = -0.00010000000100000001
# Vérification
print("ax² + bx + c = {}".format(a*x*x + b*x + c))
print("ay² + by + c = {}".format(a*y*y + b*y + c))
ax² + bx + c = 0.0
ay² + by + c = 0.0
Exercice : envisager tous les cas possibles pour le choix de a, b et c : l’écriture d’un programme numériquement robuste pour le calcul des racines d’un trinôme du second degré est loin d’être simple.
Erreurs d’arrondi
Calcul des termes d’une suite :
Calcul de $u_{n+1} = 4 u_n - 1$ avec $u_0 = 1/3$
x = 1/3
for i in range(50):
x = 4*x - 1
print(x)
0.33333333333333326
0.33333333333333304
0.33333333333333215
0.3333333333333286
0.3333333333333144
0.33333333333325754
0.33333333333303017
0.3333333333321207
0.3333333333284827
0.3333333333139308
0.3333333332557231
0.3333333330228925
0.3333333320915699
0.3333333283662796
0.3333333134651184
0.33333325386047363
0.33333301544189453
0.3333320617675781
0.3333282470703125
0.33331298828125
0.333251953125
0.3330078125
0.33203125
0.328125
0.3125
0.25
0.0
-1.0
-5.0
-21.0
-85.0
-341.0
-1365.0
-5461.0
-21845.0
-87381.0
-349525.0
-1398101.0
-5592405.0
-22369621.0
-89478485.0
-357913941.0
-1431655765.0
-5726623061.0
-22906492245.0
-91625968981.0
-366503875925.0
-1466015503701.0
-5864062014805.0
-23456248059221.0
Calcul de $u_{n+1} = 3 u_n - 1$ avec $u_0 = 1/2$
x = 1/2
for i in range(50):
x = 3*x - 1
print(x)
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
Problème mal conditionné
Résoudre un système linéaire $Ax = b$ avec $A$ quelconque
N = 40
A = np.random.rand(N, N)
b = np.arange(1, N+1)
x = np.linalg.solve(A, b)
x
array([ 4.33620564, 1.62186228, -27.19954756, 4.36455062,
-24.60731709, -11.28670069, -15.41964884, 12.18656733,
0.45112402, -3.87431386, -10.57541072, -0.23093873,
3.62740722, 8.90955365, 8.60412767, 7.34031902,
5.9230333 , 3.42822255, 1.41022622, -6.54389414,
-10.00094676, -3.77363095, 7.87430301, -26.48354662,
13.97865685, 27.29620051, 5.54632052, -8.55102887,
5.04585292, -3.29214344, -21.88860293, 6.39257995,
-1.94197313, 9.35981911, 25.8363687 , -3.36127592,
15.9989246 , 16.36192944, -24.42661185, 43.72604007])
np.max(np.abs(A @ x - b))
4.973799150320701e-14
np.linalg.cond(A)
584.8458633271287
Résoudre un système linéaire $Ax = b$ avec la matrice de Hilbert
$$A_{i,j}=\frac{1}{i+j-1}.$$
N = 40
A = np.fromfunction(lambda i, j: 1 / (i+j+1), (N, N)) # i+j+1 car i et j commencent à 0 en Python
b = np.arange(1, N+1)
x = np.linalg.solve(A, b)
x
array([ 4.87637519e+03, -7.72593266e+05, 3.03428996e+07, -5.17019809e+08,
4.75675321e+09, -2.63265691e+10, 9.20658875e+10, -2.02259559e+11,
2.50344415e+11, -9.34102481e+10, -9.14799063e+10, -1.69941076e+11,
6.49204839e+11, -4.12056938e+11, -1.62136188e+11, -1.60962818e+10,
2.02941397e+11, 8.08402238e+10, -1.13280864e+11, 2.25134855e+11,
-1.83742135e+11, 1.35707012e+11, -6.90181450e+11, 6.03023373e+11,
-5.93352918e+11, 6.69302159e+11, 1.90231397e+11, -5.04236249e+10,
-4.17557593e+10, -4.54270557e+11, 1.89362489e+11, -1.20319327e+11,
-2.92749525e+11, 2.34680270e+11, 1.96469712e+11, 1.97768878e+11,
6.60265142e+11, -1.48402608e+12, 5.98386259e+11, 1.78115288e+10])
np.max(np.abs(A @ x - b))
2.288818359375e-05
np.linalg.cond(A)
9.220953338051718e+18
Résoudre un système linéaire $Ax = b$ avec la matrice du Laplacien 1D
Résoudre $$\Delta u = 0$$ avec $$\Delta u(x) \approx \frac{u(x-h) - 2u(x) + u(x+h)}{h^2}.$$
N = 40
A = np.diag(np.ones(N-1), 1) + np.diag(np.ones(N-1), -1) - 2 * np.eye(N, N)
b = np.arange(1, N+1)
x = np.linalg.solve(A, b)
x
array([ -280., -559., -836., -1110., -1380., -1645., -1904., -2156.,
-2400., -2635., -2860., -3074., -3276., -3465., -3640., -3800.,
-3944., -4071., -4180., -4270., -4340., -4389., -4416., -4420.,
-4400., -4355., -4284., -4186., -4060., -3905., -3720., -3504.,
-3256., -2975., -2660., -2310., -1924., -1501., -1040., -540.])
np.max(np.abs(A @ x - b))
1.8189894035458565e-12
np.linalg.cond(A)
680.6170700217184